Trikonmiti Formula किसी भी प्रतियोगी परीक्षा जैसे SSC परीक्षा, Railway परीक्षा, Bank परीक्षा आदि या स्कूली परीक्षा के लिए महत्वपूर्ण होते हैं।
इन Trikonmiti Formula को स्कूल की परीक्षाओं के लिए भी याद करना जरूरी है। SSC की परीक्षा में त्रिकोणमिति से संबंधित कई प्रश्न पूछे जाते हैं। इसलिए यदि आप SSC की तैयारी कर रहे हैं तो हर एक Trikonmiti ka Formula आपके लिए बहुत उपयोगी है।
Table of Contents
- 1. Trigonometry in Hindi / त्रिकोणमिति क्या है?
- 2. महत्वपूर्ण Trikonmiti Formula / Trikonmiti ka Sutra
- 2.1. त्रिकोणमितिय अनुपात / Trigonometric Ratios
- 2.2. त्रिकोणमितिय अनुपातों के बीच पारस्परिक सम्बन्ध (Reciprocal Relations)
- 2.3. Trikonmiti table / Trigonometry Table
- 3. त्रिकोणमितीय सर्वसमिकाएँ (Trigonometric Identities या Pythagorean Identities)
- 3.1. पूरक कोणों के त्रिकोणमितीय अनुपात (Cofunction Identities)
- 3.2. आवर्तता सर्वसमिकाएँ (Periodicity Identities)
- 3.3. अन्य आवर्तता सर्वसमिकाएँ
- 3.4. सम और विषम कोण सूत्र (Even and Odd Angle Trikonmiti Formula)
- 3.5. द्विकोण फार्मूला ( Double Angle Trikonmiti Formula )
- 3.6. कोणों के योग और अंतर की त्रिकोणमितीय सर्वसमिकाएं
- 3.7. गुणक से जोड़ की सर्वसमिकाएं (Product to Sum Identities)
- 3.8. जोड़ से गुणक की सर्वसमिकाएं (Sum to Product Identities)
- 4. सम त्रिकोणमितीय फलन (Even Trigonometric Functions)
- 4.1. प्रतिलोम त्रिकोणमितीय फलन (Inverse Trigonometry Formulas)
- 4.2. अर्द्ध कोण सर्वसमिकाएँ (Half angle identities)
- 5. Trigonometry Important Questions in Hindi
- 6. Trikonmiti formula से संबंधित FAQs
इन Trikonmiti Formula का उपयोग करके त्रिकोणमिति से संबंधित प्रश्नों को हल किया जाता है। इस लेख में हमनें विभिन्न परीक्षाओं के लिए महत्वपूर्ण Trikonmiti Formula उपलब्ध कराया है।
Trikonmiti Formula याद होने से प्रश्नों को जल्दी से हल भी किया जा सकता है। इसलिए इस लेख में दिए गए सभी Trikonmiti Formula या trikonmiti ka sutra को याद कर लें।
यह भी पढ़ें - > सरकारी नौकरी की तैयारी कैसे करें? > SSC CGL की तैयारी कैसे करें?
Trigonometry in Hindi / त्रिकोणमिति क्या है?
Trikonmiti Formula जानने से पहले आपको यह जरूर जानना चाहिए कि Trigonometry meaning in Hindi क्या है?
Trigonometry शब्द की व्युत्पत्ति ग्रीक शब्दों Tri (जिसका अर्थ है तीन), “gon” (जिसका अर्थ है, भुजा) और ‘metron’ (जिसका अर्थ है माप) से हुई है।
त्रिकोणमिति के अंतर्गत किसी त्रिभुज की भुजाओं और कोणों के बीच के संबंधों का अध्ययन किया जाता है। त्रिकोणमिति का प्रयोग प्राचीन काल से चला आ रहा है। प्राचीन काल में मिस्र और बेबीलॉन के लोगों द्वारा त्रिकोणमिति के उपयोग का साक्ष्य मिलता है।
प्राचीन काल के खगोलविद् त्रिकोणमिति का प्रयोग पृथ्वी से तारों और ग्रहों की दूरियाँ मापने में करते थे। आज के आधुनिक इंजीनियरिंग और भौतिक विज्ञान में भी त्रिकोणमिति का उपयोग किया जाता है।
महत्वपूर्ण Trikonmiti Formula / Trikonmiti ka Sutra
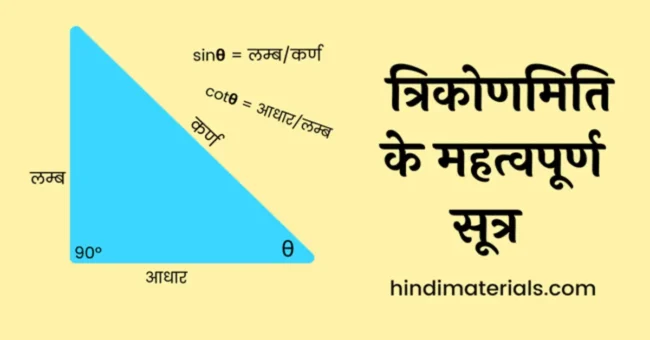
जब हम Trikonmiti Formula के बारे में सीखते हैं तो सभी फॉर्मूले हम एक समकोण त्रिभुज के लिए ही निकालते हैं।
जैसे कि आपको पता होगा कि एक समकोण त्रिभुज (right-angled triangle) में तीन भुजायें (sides) होती हैं – आधार, लम्ब और कर्ण।
जैसा कि नीचे चित्र में देख सकते हैं कि त्रिकोण की क्षैतिज भुजा को आधार (Base) कहा जाता है। आधार के साथ 90 डिग्री का कोण बनाने वाली भुजा को लम्ब (Perpendicular) कहा जाता है और 90 डिग्री के सामने वाली शेष भुजा को कर्ण (Hypotenuse) कहते हैं।
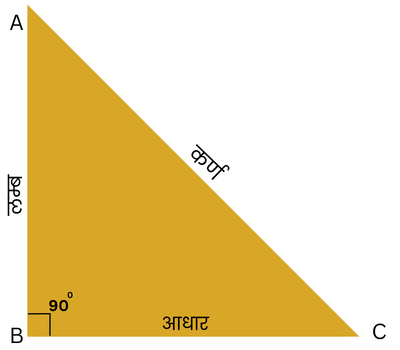
त्रिकोणमितिय अनुपात / Trigonometric Ratios
त्रिकोणमितिय अनुपातों का प्रयोग त्रिकोणमिति से संबंधित सभी प्रश्नों को हल करने में किया जाता है। इन्हें Trigonometric Functions भी कहा जाता है। ये बेसिक Trikonmiti Formula होते हैं।
त्रिकोणमितिय अनुपात 6 प्रकार के होते है – Sine (ज्या), Cosine (कोज्या), Tangent (स्पर्शज्या), Co-secant (व्युज्या), Secant (व्युकोज्या) और Co-tangent (व्युस्पर्शज्या)। इनका संक्षिप्त रूप हैं – sin, cos, tan, cosec, sec और cot.
अब हम ऊपर दिए गए समकोण के आधार पर त्रिकोणमितिय अनुपात निकलेंगे।
सबसे पहले हम Basic Trikonmiti Formula के बारे में बताएंगे, जो इस प्रकार हैं
sinθ = लम्ब/कर्ण = perpendicular / hypotenuse
cosθ = आधार/कर्ण = base / hypotenuse
tanθ = लम्ब/आधार = perpendicular / base
cotθ = आधार/लम्ब = base / perpendicular
secθ = कर्ण/आधार = hypotenuse / base
coescθ = कर्ण/लम्ब = hypotenuse / perpendicular
इन Trikonmiti Formula का प्रयोग तब होता है जब आपको समकोण त्रिभुज के भुजाओं की लंबाई पता हों या एक कोण और एक भुजा की लंबाई मालूम हो और दूसरी भुजा की लंबाई निकालनी हो।
त्रिकोणमितिय अनुपातों के बीच पारस्परिक सम्बन्ध (Reciprocal Relations)
sinθ = 1 / Cosecθ या Sin θ × Cosecθ = 1
Cosecθ = 1 / sinθ या Cosecθ × Sin θ = 1
Cosθ = 1 / Secθ या Cos θ × Sec θ = 1
Secθ = 1 / Cosθ या Sec θ × Cos θ = 1
Tanθ = 1 / Cotθ या Tan θ × Cot θ = 1
Cotθ = 1 / Tanθ या Cot θ × Tan θ = 1
इन Trikonmiti Formula का प्रयोग तब होता है जब किसी एक त्रिकोणमितीय अनुपात का मान ज्ञात हो और दूसरे त्रिकोणमितीय अनुपात का मान निकालना हो। जैसे यदि आप किसी कोण के cosec का मान जानते हैं तो आसानी से उसके sin का मान निकाल सकते हैं।
Trikonmiti table / Trigonometry Table
यदि आपको किसी त्रिकोण के एक कोण का मान मालूम हो तो नीचे दिए गए Trikonmiti table की सहायता से त्रिकोणमितीय अनुपातों जैसे sin, cos, tan, cosec, sec और cot का मान निकाल सकते हैं।
परीक्षा में पूछे जाने वाले अधिकतर प्रश्नों को आप इस टेबल के द्वारा हल कर सकते हैं। इसलिए छात्रों को सलाह दी जाती है कि Trikonmiti Formula के साथ-साथ इस टेबल को अच्छी तरह से याद कर लें।
| कोण | 0° | 30° या π/6 | 45° या π/4 | 60° या π/3 | 90° या π/2 | 180° या π | 270° या 3π/2 | 360° या 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
त्रिकोणमितीय सर्वसमिकाएँ (Trigonometric Identities या Pythagorean Identities)
जैसा कि आपको पता होगा कि एक समीकरण को एक सर्वसमिका तब कहा जाता है जबकि यह संबंधित चरों के सभी मानों के लिए सत्य हो।
इसी प्रकार एक कोण के त्रिकोणमितीय अनुपातों से संबंधित सर्वसमिका को त्रिकोणमितीय सर्वसमिका कहा जाता है। जबकि यह संबंधित कोण (कोणों) के सभी मानों के लिए सत्य होता हे।
ये सर्वसमिकाएं Pythagorean Theorem को फॉलो करती हैं इसलिए इन्हें Pythagorean Identities भी कहते हैं। अब आईए जानते हैं कौन-कौन से त्रिकोणमितीय सर्वसमिकाएं हैं-
| sin²θ + cos²θ = 1 |
| sin²θ = 1 – cos²θ |
| cos²θ = 1- sin²θ |
| Sec²θ – Tan²θ = 1 |
| 1 + tan²θ = sec²θ |
| Sec²θ –1 = Tan²θ |
| cosec²θ = cot²θ + 1 |
| sinθ = √(1 – cos²θ) |
| cosθ = √( sinθ – 1 ) |
| tan²θ = sec²θ – 1 |
| tanθ = √(sec²θ – 1) |
| secθ = √(1 + tan²θ) |
| cosecθ = √(cot²θ + 1) |
| cot²θ = cosec²θ – 1 |
| cot²θ = √(cosec²θ – 1) |
पूरक कोणों के त्रिकोणमितीय अनुपात (Cofunction Identities)
एक त्रिभुज के दो कोणों को पूरक कोण तब कहा जाता है जब उनका योग 90 डिग्री के बराबर हो जाता है।
| रेडियन में | डिग्री में |
| sin (π/2 – θ) = cos θ | sin (90° – θ) = cos θ |
| cos (π/2 – θ) = sin θ | cos (90° – θ) = sin θ |
| tan (π/2 – θ) = cot θ | tan (90° – θ) = cot θ |
| cot (π/2 – θ) = tan θ | cot (90° – θ) = tan θ |
| sec (π/2 – θ) = cosec θ | sec (90° – θ) = cosec θ |
| cosec (π/2 – θ) = sec θ | cosec (90° – θ) = sec θ |
आवर्तता सर्वसमिकाएँ (Periodicity Identities)
इन Trikonmiti Formula का प्रयोग हम कोणों को π/2, π, 2π, 3π/2 आदि द्वारा शिफ्ट करने के लिए करते हैं।
π/2 द्वारा shifting
| रेडियन में | डिग्री में |
| sin (π/2 + θ) = +cos θ | Sin (900 + θ) = Cos θ |
| cos (π/2 + θ) = – sin θ | Cos (900 + θ) = – Sin θ |
| tan (π/2 + θ) = -cot θ | Tan (900 + θ) = – Cot θ |
| cot (π/2 + θ) = -tan θ | Cot (900 + θ) = – Tan θ |
| sec (π/2 + θ) = -cosec θ | Sec (900 + θ) = – Cosec θ |
| cosec (π/2 + θ) = +sec θ | Cosec (900+θ) = Sec θ |
π द्वारा shifting
| रेडियन में | डिग्री में |
| sin (π + θ) = – sin θ | Sin (1800 + θ) = – Sin θ |
| cos (π + θ) = – cos θ | Cos (1800 + θ) = – Cos θ |
| tan (π + θ) = + tan θ | Tan (1800 + θ) = + Tan θ |
| cot (π + θ) = + cot θ | Cot (1800 + θ) = + Cot θ |
| sec (π + θ) = – sec θ | Sec (1800 + θ) = – Sec θ |
| cosec (π + θ) = – cosec θ | Cosec (1800+θ) = -Cosec θ |
2π द्वारा shifting
| रेडियन में | डिग्री में |
| sin (2π + θ) = + sin θ | Sin (3600 + θ) = Sin θ |
| cos (2π + θ) = + cos θ | Cos (3600 + θ) = Cos θ |
| tan (2π + θ) = + tan θ | Tan (3600 + θ) = Tan θ |
| cot (2π + θ) = + cot θ | Cot (3600 + θ) = Cot θ |
| sec (2π + θ) = + sec θ | Sec (3600 + θ) = Sec θ |
| cosec (2π + θ) = + cosec θ | Cosec (3600+θ) = Cosec θ |
अन्य आवर्तता सर्वसमिकाएँ
| रेडियन में | डिग्री में |
| sin (π – θ) = +sin θ | Sin (1800 – θ) = Sin θ |
| cos (π – θ) = – cos θ | Cos (1800 – θ) = – Cos θ |
| tan (π – θ) = – tan θ | Tan (1800 – θ) = – Tan θ |
| cot (π – θ) = – cot θ | Cot (1800 – θ) = – Cot θ |
| sec (π – θ) = -sec θ | Sec (1800 – θ) = – Sec θ |
| cosec (π – θ) = + cosec θ | Cosec (1800-θ)= Cosec θ |
| रेडियन में | डिग्री में |
| sin (3π/2 – θ) = – cos θ | Sin (2700 – θ) = – Cos θ |
| cos (3π/2 – θ) = – sin θ | Cos (2700 – θ) = – Sin θ |
| Tan (3π/2 – θ) = + Cot θ | Tan (2700 – θ) = + Cot θ |
| Cot (3π/2 – θ) = + Tan θ | Cot (2700 – θ) = + Tan θ |
| Sec (3π/2 – θ) = – Cosec θ | Sec (2700 – θ) = – Cosec θ |
| Cosec (3π/2 – θ)= -Sec θ | Cosec (2700-θ)= -Sec θ |
| रेडियन में | डिग्री में |
| Sin (3π/2 + θ) = – Cos θ | Sin (2700 + θ) = – Cos θ |
| Cos (3π/2 + θ) = + Sin θ | Cos (2700 + θ) = + Sin θ |
| Tan (3π/2 + θ) = – Cot θ | Tan (2700 + θ) = – Cot θ |
| Cot (3π/2 + θ) = – Tan θ | Cot (2700 + θ) = – Tan θ |
| Sec (3π/2 + θ) = + Cosec θ | Sec (2700 + θ) = + Cosec θ |
| Cosec (3π/2 + θ) = – Sec θ | Cosec (2700+θ) = – Sec θ |
| रेडियन में | डिग्री में |
| Sin (2π – θ) = – Sin θ | Sin (3600 – θ) = – Sin θ |
| Cos (2π – θ) = + Cos θ | Cos (3600 – θ) = + Cos θ |
| Tan (2π – θ) = – Tan θ | Tan (3600 – θ) = – Tan θ |
| Cot (2π – θ) = – Cot θ | Cot (3600 – θ) = – Cot θ |
| Sec (2π – θ) = + Sec θ | Sec (3600 – θ) = + Sec θ |
| Cosec (2π – θ)= – Cosec θ | Cosec (3600– θ)= – Cosec θ |
सम और विषम कोण सूत्र (Even and Odd Angle Trikonmiti Formula)
• sin(−θ) = − sinθ
• cos(−θ) = cosθ
• tan(−θ) = − tanθ
• cosec(−θ) = − cosecθ
• sec(−θ) = secθ
• cot(−θ) = − cotθ
द्विकोण फार्मूला ( Double Angle Trikonmiti Formula )
यहाँ द्विकोण यानि double angle का मतलब है किसी कोण का दुगुना। Trikonmiti Formula में Double Angle Formula भी हैं जिनमें से कुछ प्रमुख फॉर्मूले इस प्रकार से हैं-
sin 2θ = 2 sin θ cos θ = (2 tan θ) / (1 + tan2θ)
cos 2θ = cos²θ – sin²θ = 2cos2θ – 1 = 1 – 2sin2 θ = (1 – tan2θ) / (1 + tan2θ)
tan 2θ = 2 tan θ / (1 – tan²θ)
cot 2θ = (cot²θ – 1) / 2 cot θ
sec 2θ = sec2θ/2- sec2θ
cosec 2θ = secθ.cosecθ/2
यदि कोणों को तीन गुना कर दिया जाए तो निम्नलिखित सूत्र प्राप्त होते हैं –
• sin 3θ = 3sin θ – 4sin3 θ
• cos 3θ = 4cos3 θ – 3cos θ
• tan 3θ = (3tan θ – tan3 θ) / (1 – 3tan2 θ)
• cos 3θ = (cos3θ – 3cos3 θ)/( 3cos2 θ -1)
कोणों के योग और अंतर की त्रिकोणमितीय सर्वसमिकाएं
• sin(A+B) = sin A . cos B + cos A . sin B
• cos (A+B) = cos A . cos B − sin A . sin B
• tan (A + B) = (tan A + tan B) / ( 1 − tan A . tan B)
• cot (A + B) = (cot A . cot B − 1) / (cot B + cot A)
• sin(A-B) = sin A . cos B − cos A . sin B
• cos (A-B) = cos A . cos B + sin A . sin B
• tan(A – B)= ( tan A – tan B )/ ( 1 + tan A . tan B )
• cot(A – B) = (cot A . cot B + 1) / ( cot B – cot A )
गुणक से जोड़ की सर्वसमिकाएं (Product to Sum Identities)
2sin A . sin B = cos(A – B) – cos(A + B)
2sin A . cos B = sin(A + B) + sin(A – B)
2cos A . sin B = sin(A + B) – sin(A – B)
2cos A . cos B = cos(A + B) + cos(A – B)
जोड़ से गुणक की सर्वसमिकाएं (Sum to Product Identities)
sinA + sinB = 2[sin((A + B)/2)cos((A − B)/2)]
sinA − sinB = 2[cos((A + B)/2)sin((A − B)/2)]
cosA + cosB = 2[cos((A + B)/2)cos((A − B)/2)]
cosA − cosB = −2[sin((A + B)/2)sin((A − B)/2)]
सम त्रिकोणमितीय फलन (Even Trigonometric Functions)
एक त्रिकोणमितीय फलन सम फलन तब कहा जाता है यदि f(-x) = f(x) हो।
Sin (-x) = – Sin x
Cos (-x) = Cos x
Tan (-x) = -Tan x
Cosec (-x) = – Cosec x
Sec (-x) = Sec x
Cot (-x) = -Cot x
प्रतिलोम त्रिकोणमितीय फलन (Inverse Trigonometry Formulas)
sin-1 (-x) = -sin-1 x
cos-1 (-x) = π – cos-1 x
tan-1 (-x) = -tan-1 x
cosec-1 (-x) = -cosec-1 x
sec-1 (-x) = π – sec-1 x
cot-1 (-x) = π – cot-1 x
अर्द्ध कोण सर्वसमिकाएँ (Half angle identities)
• Sin θ = 2 sin(θ/2) . cos(θ/2)
• Cos θ = [cos2 (θ/2)- sin2(θ/2)]= [2 cos2(θ/2) – 1] = [1 – 2 sin2(θ/2)]
• cos θ = [{1- tan2(θ/2)}/ {1 + tan2(θ/2)}]
• tan θ = [{2 tan (θ/2)} / {1- tan2(θ/2)}]
sin(A/2) = +/- √((1 – cos(A))/2)
cos(A/2) = +/-√((1 + cos(A))/2)
tan(A/2) = +/- √((1 – cos(A))/(1 + cos(A))
Trigonometry Important Questions in Hindi
अब हम ऊपर बताए गए Trikonmiti Formula के आधार पर कुछ महत्वपूर्ण प्रश्न और उन्हें हल करने जा रहे हैं। ये प्रश्न SSC Exams के लिए भी महत्वपूर्ण हैं।
प्रश्न 1. नीचे दिए गए त्रिभुज से tan A और cot C का मान निकालें।

हल – जैसा कि चित्र में दिए गए समकोण त्रिभुज का लम्ब 12cm और कर्ण 13cm है। सबसे पहले Pythagoras प्रमेय से दिए त्रिभुज के आधार की लंबाई ज्ञात करेंगे। Pythagoras प्रमेय – AC2 = AB2 + BC2 BC2 = AC2 – AB2 BC2 = (13)2 – (12)2 = 169 – 144 = 25 अतः BC = 5 cm अब Trikonmiti Formula के अनुसार tan A = लम्ब / आधार = BC/AB = 5/12 और cot C = आधार / लम्ब = BC/AB = 5/12
प्रश्न-2 : यदि A, B और C किसी त्रिभुज ABC के आंतरिक कोण हैं तो सिद्ध कीजिए कि sin (B + C/2) = cos A/2.
हल - हम जानते हैं कि किसी दिए गए त्रिभुज के लिए, त्रिभुज के सभी आंतरिक कोणों का योग 180° के बराबर होता है। अतः A + B + C = 180° या B + C = 180° – A दोनों तरफ 2 से भाग देने पर- ⇒ (B + C)/2 = (180° – A)/2 ⇒ (B + C)/2 = 90° – A/2 दोनों तरफ sin लेने पर- sin (B + C)/2 = sin (90° – A/2) ⇒ sin (B + C)/2 = cos A/2 (Trikonmiti Formula sin(90° – θ) = cos θ) के अनुसार) सिद्ध हुआ।
प्रश्न -3– यदि sin 3A = cos (A – 26°), जहाँ 3A एक न्यून कोण है, तो कोण A का मान निकालें।
हल: दिया गया है- sin 3A = cos(A – 26°); जहाँ 3A एक न्यून कोण है। या cos(90° – 3A) = cos(A – 26°) (Trikonmiti Formula since cos(90° – θ) = sin θ के अनुसार) ⇒ 90° – 3A = A – 26 ⇒ 3A + A = 90° + 26° ⇒ 4A = 116° ⇒ A = 116°/4 ⇒ A = 29° उत्तर- कोण A = 29°
प्रश्न -4- यदि tan(A + B) = √3 और tan(A – B) = 1/√3 ; 0° < A + B ≤ 90°; A > B, तो A और B का मान ज्ञात करें।
हल- प्रश्न के अनुसार tan(A + B) = √3 या tan(A + B) = tan 60° (चूंकि tan 60° = √3 ) अतः A + B = 60°……….समीकरण (i) और tan(A – B) = 1/√3 या tan(A – B) = tan 30° (चूंकि tan 30° = 1/√3 ) अतः A – B = 30°….…….समीकरण (ii) समीकरण (i) और (ii) का योग- A + B + A – B = 60° + 30° 2A = 90° A = 45° अब A के इस मान को समीकरण (i) में रखेंगे- 45° + B = 60° B = 60° – 45° = 15° इस तरह कोण A = 45° और कोण B = 15°
प्रश्न -5- यदि tan θ + sec θ = m, तो सिद्ध करें कि sec θ = (m2 + 1)/2m
हल-
दिया है कि –
tan θ + sec θ = m…………समीकरण(i)
हम जानते हैं कि-
sec2θ – tan2θ = 1
(sec θ – tan θ)(sec θ + tan θ) = 1 {Trikonmiti Formula a2 – b2 = (a – b)(a + b) के अनुसार}
(sec θ – tan θ) m = 1 (समीकरण (i) से)
sec θ – tan θ = 1/m………समीकरण (ii)
समीकरण (i) और (ii) को जोड़ने पर -
tan θ + sec θ + sec θ – tan θ = m + (1/m)
2 sec θ = (m2 + 1)/m
sec θ = (m2 + 1)/2m
अतः सिद्ध हुआ। प्रश्न – 6- यदि a sin θ + b cos θ = c, तो सिद्ध कीजिए कि a cosθ – b sinθ = √(a2 + b2 – c2).
हल: दिया गया है कि- a sin θ + b cos θ = c दोनों पक्षों का वर्ग करने पर, (a sin θ + b cos θ)2 = c2 a2 sin2θ + b2 cos2θ + 2ab sin θ cos θ = c2 हम जानते हैं कि sin2A + cos2A = 1 या sin2A = 1 - cos2A और cos2A = 1 - sin2A अतः- a2(1 – cos2θ) + b2(1 – sin2θ) + 2ab sin θ cos θ = c2 ⇒ a2 – a2 cos2θ + b2 – b2 sin2θ + 2ab sin θ cos θ = c2 ⇒ a2 + b2 – c2 = a2 cos2θ + b2 sin2θ – 2ab sin θ cos θ ⇒ a2 + b2 – c2 = (a cos θ – b sin θ )2 ⇒ a cos θ – b sin θ = √(a2 + b2 – c2) अतः सिद्ध हुआ।
प्रश्न – 7- किसी त्रिभुज ∆ ABC में कोण B समकोण है, और AB = 24 cm, BC = 7 cm तो sin A, sin C, cos A और cos C का मान निकालें।

हल- दिए गए समकोण त्रिभुज में B = 90° है। तो AC2 = AB2 + BC2 AC2 = (24)2 + 72 AC2 = (576 + 49) AC2 = 625 cm2 AC = 25 cm अतः Sin A = लम्ब / कर्ण = 7/25 cos A = आधार/कर्ण = AB/AC = 24/25 Sin C = लम्ब / कर्ण = AB/AC = 24/25 Cos C = आधार/कर्ण = BC/AC = 7/25
प्रश्न 8: यदि Sin A = 3/4 तो cos A और tan A का मान ज्ञात करें।
हल: माना कि ABC एक समकोण त्रिभुज है और कोण B = 900 है। दिया हुआ है कि Sin A = 3/4 जैसा कि हम जानते हैं कि Sin A = लम्ब/कर्ण = 3/4 अतः Pythagoras प्रमेय के अनुसार आधार2 = 42 – 32 या 16 – 9 = 7 आधार = √7 अतः cos A = √7 /4 और tan A = 3/√7
प्रश्न 9: किसी त्रिभुज में यदि ∠A और ∠B न्यून कोण हैं और cos A = cos B, तो सिद्ध करें कि ∠ A = ∠ B
हल: माना कि त्रिभुज ABC में कोण C समकोण है, तो cos A = AC/AB cos B = BC/AB चूंकि दिया हुआ है कि cos A = cos B तो AC/AB = BC/AB AC = BC इससे यह सिद्ध होता है कि त्रिभुज ABC एक समद्विबाहु त्रिभुज है और समद्विबहुत त्रिभुज की परिभाषा के अनुसार दो समान भुजाओं के विपरीत कोण बराबर होते हैं। इसलिए ∠A = ∠B सिद्ध हुआ।
प्रश्न 10 : एक त्रिभुज PQR में कोण Q समकोण है, जिसमें PR + QR = 25 cm और PQ = 5 cm है। तो sin P, cos P और tan P का मान ज्ञात करें।
हल: दिया हुआ है कि त्रिभुज PQR में PQ = 5 cm और PR + QR = 25 cm है। माना कि QR = x cm तब PR = 25 – QR = 25 – x तो Pythagoras प्रमेय के अनुसार- PR2 = PQ2 + QR2 PR, PQ और QR का मान रखने पर- (25 – x)2 = (5)2 + (x)2 252 + x2 – 50x = 25 + x2 625 – 50x = 25 50x = 600 x = 12 अतः, QR = 12 cm PR = 25 – QR = 25 – 12 = 13 cm इसलिए, sin P = QR/PR = 12/13 cos P = PQ/PR = 5/13 tan P = QR/PQ = 12/5
प्रश्न 11 : 2 tan2 45° + cos2 30° – sin2 60° का मान ज्ञात करें।
हल: ऊपर दिए गए Trigonometry table से- tan 45° = 1 cos 30° = √3/2 sin 60° = √3/2 इसलिए, इनका मान प्रश्न में दिए गए समीकरण में रखने पर- 2(1)2 + (√3/2)2 – (√3/2)2 = 2 + 0 = 2
प्रश्न 12 : यदि tan (A + B) =√3 और tan (A – B) =1/√3, जहाँ 0° < A + B ≤ 90°; A > B, तो A और B का मान ज्ञात करें।
हल: दिया गया है कि- tan (A + B) = √3 और tan (A – B) =1/√3 Trigonometry Table से, tan 60° = √3 और tan 30° = 1/√3 ऊपर दिए समीकरणों में रखने पर tan (A + B) = √3 ⇒ tan (A + B) = tan 60° ⇒(A + B) = 60° …………समीकरण(i) और tan (A – B) = 1/√3 ⇒ tan (A – B) = tan 30° ⇒(A – B) = 30° ….. समीकरण (ii) समीकरण (i) और (ii) को जोड़ने पर- A + B + A – B = 60° + 30° 2A = 90° A= 45° अब A का मान समीकरण (i) में रखने पर 45° + B = 60° B = 60° – 45° B = 15° इसलिए, A = 45° और B = 15°
प्रश्न 13 : सिद्ध करें कि: (i) tan 48° tan 23° tan 42° tan 67° = 1 (ii) cos 38° cos 52° – sin 38° sin 52° = 0
हल:
(i) tan 48° tan 23° tan 42° tan 67° में
tan 48° = tan (90° – 42°) = cot 42° {चूंकि cot θ= tan (90°- θ)}
और tan 23° = tan (90° – 67°) = cot 67°
अतः, tan 48° tan 23° tan 42° tan 67°
= cot 42° cot 67° tan 42° tan 67°
= (cot 42° tan 42°) (cot 67° tan 67°)
= 1 × 1 [चूंकि cot A.tan A = 1]
= 1
(ii) cos 38° cos 52° – sin 38° sin 52° में
cos 38° = cos (90° – 52°) = sin 52° {चूंकि sin θ = cos(90°- θ)}
और
cos 52°= cos (90° – 38°) = sin 38°
अतः
sin 52° sin 38° – sin 38° sin 52° = 0
प्रश्न 14 :यदि tan 2A = cot (A – 18°), जहाँ 2A एक न्यून कोण है, तो Aका मान ज्ञात करें।
हल: दिया गया है- tan 2A = cot (A – 18°) त्रिकोणमितीय सर्वसमिका के अनुसार tan 2A = cot (90° – 2A) इसे दिए गए समीकरण में रखने पर cot (90° – 2A) = cot (A – 18°) इसलिए- 90° – 2A = A – 18° 108° = 3A A = 108° / 3 इसलिए A = 36°
प्रश्न 15 : यदि A, B और C किसी त्रिभुज ABC के आंतरिक कोण हैं तो सिद्ध करें कि sin [(B + C)/2] = cos A/2
हल: जैसा कि हमें पता है कि किसी त्रिभुज के तीनों आंतरिक कोणों का योग 180° होता है। अतः, A + B + C = 180° …….समीकरण (i) या B + C = 180° – A अब दोनों तरफ 2 से भाग देने पर- ⇒ (B + C)/2 = (180° – A)/2 ⇒ (B + C)/2 = 90° – A/2 अब दोनों तरफ sin लेने पार ⇒ sin (B + C)/2 = sin (90° – A/2) या sin (B + C)/2 = cos A/2 (चूंकि sin(90°- θ) = cos θ)
Important Tags – trikonmiti formula, all trikonmiti formula, trikonmiti formula trick, trikonmiti ka formula, trikonmiti sutra, trigonometry formula, trikonmiti formula list, trigonometry all formula, trikonmiti formulas, trikonmiti formula in hindi, trikonmiti class 10 formula
Trikonmiti formula से संबंधित FAQs
त्रिकोणमिति में एक कोण का sine, cosine और tangent क्या है?
एक समकोण त्रिभुज के कोण की ज्या (sine) कोण के विपरीत भुजा की लंबाई से कर्ण की लंबाई का अनुपात होता है। जबकि उस कोण की कोज्या (cosine) कोण के निकटवर्ती भुजा की लंबाई से कर्ण की लंबाई अनुपात होता है और कोण की स्पर्शज्या (tangent) sine से cosine का अनुपात होता है।
त्रिकोणमितिय अनुपात (Trigonometry ratio) कितने प्रकार के होते हैं?
त्रिकोणमितिय अनुपात 6 प्रकार के होते है – Sine (ज्या), Cosine (कोज्या), Tangent (स्पर्शज्या), Co-secant (व्युज्या), Secant (व्युकोज्या) और Co-tangent (व्युस्पर्शज्या)। इनका संक्षिप्त रूप हैं – sin, cos, tan, cosec, sec और cot.
त्रिकोणमिति में पाइथागोरस प्रमेय (Pythagorean theorem) क्या होता है?
पाइथागोरस प्रमेय के अनुसार किसी समकोण त्रिभुज में कर्ण का वर्ग, अन्य दो भुजाओं के वर्ग के योग के बराबर होता है। यदि कर्ण c है और अन्य दो भुजायें a और b हैं तो पाइथागोरस प्रमेय के अनुसार c2 = a2 + b2. त्रिकोणमिति में इस प्रमेय का प्रयोग अक्सर किसी समकोण त्रिभुज के किसी भुजा की लंबाई ज्ञात करने में किया जाता है।
त्रिकोणमिति में sine, cosine, और tangent का double angle formula क्या होता है?
त्रिकोणमिति में double angle formulas से किसी कोण के दोगुने के sine, cosine, or tangent ज्ञात किया जाता है। double angle formulas इस प्रकार हैं:
sin(2A) = 2sin(A)cos(A)
cos(2A) = cos2(A) – sin2(A) = 2cos2(A) – 1 = 1 – 2sin2(A)
tan(2A) = 2tan(A)/(1 – tan2(A))
त्रिकोणमिति में sine, cosine, और tangent का half angle formula क्या होता है?
त्रिकोणमिति में half angle formulas से किसी कोण केआधे के sine, cosine, or tangent ज्ञात किया जाता है। half angle formulas इस प्रकार हैं:
sin(A/2) = ±√[(1 – cos A) / 2]
cos(A/2) = ±√[(1 + cos A) / 2]
tan(A/2) = ±√[1 – cos A] / [1 + cos A] या sin A / (1 + cos A) (or) (1 – cos A) / sin A
कुछ महत्वपूर्ण त्रिकोणमित्तीय सर्वसमिकाएँ (Trigonometric Identities) कौन-कौन से हैं?
कुछ महत्वपूर्ण त्रिकोणमितीय सर्वसमिकाएं हैं-
sin²θ + cos²θ = 1
sin²θ = 1 – cos²θ
cos²θ = 1- sin²θ
Sec²θ – Tan²θ = 1
1 + tan²θ = sec²θ
Sec²θ –1 = Tan²θ
cosec²θ = cot²θ + 1
sinθ = √(1 – cos²θ)
cosθ = √( sinθ – 1 )
tan²θ = sec²θ – 1
tanθ = √(sec²θ – 1)
secθ = √(1 + tan²θ)
cosecθ = √(cot²θ + 1)
cot²θ = cosec²θ – 1
cot²θ = √(cosec²θ – 1)

![SSC CGL Exam Pattern in Hindi [Updated 2024] SSC CGL Exam Pattern in Hindi for Tier 1 and Tier 2](https://hindimaterials.com/wp-content/uploads/2023/07/SSC-CGL-Exam-Pattern-650x340.webp)

